Texas Holdem Hand Odds Probabilities

1. Texas Holdem Hand Odds Probabilities Chart
2. Texas Holdem Hand Odds Probabilities Odds

Introduction

In Texas Hold 'Em a hand is said to be dominated if another player has a similar, and better, hand. To be more specific, a dominated hand is said to rely on three or fewer outs (cards) to beat the hand dominating it, not counting difficult multiple-card draws. There are four types of domination, as follows.

Those are the probabilities and odds for all 5-card poker hands: Poker Hand Odds for Texas Hold’em If you’re playing Texas Hold’em, you have 7 cards to chose your hand from. There are 133,784,560 to deal 7 random cards. Poker odds give you the probability of winning any given hand. Higher odds mean a lower chance of winning, meaning that when the odds are large against you it’ll be a long time until you succeed. They are usually displayed as a number to number ratio and indicate the potential return on investment; for example, odds of nine to one (9:1) means. Texas Hold'Em Dominated Hand Probabilities Introduction. In Texas Hold 'Em a hand is said to be dominated if another player has a similar, and better, hand. To be more specific, a dominated hand is said to rely on three or fewer outs (cards) to beat the hand dominating it, not counting difficult multiple-card draws. Poker hands odds & outs: a crash course-guide on poker odds, pot odds, probabilities & odds charts so you can win at Texas Hold’em at the tables or online. One of the most important things that a poker player should know is what their poker odds are in a given situation.

1. A pair is dominated by a higher pair. For example J-J is dominated by Q-Q. Only two cards help the J-J, the other two jacks.
2. A non-pair is dominated by a pair of either card. For example, Q-5 is dominated by Q-Q or 5-5. In the case of 5-5, three cards only will help the Q-5, the other three queens.
3. A non-pair is dominated by a pair greater than the lower card. For example, Q-5 is dominated by 8-8. Only three cards will help the Q-5, the other three queens.
4. A non-pair is dominated by another non-pair if there if there is a shared card, and the rank of the opponent's non-shared card is greater the dominated non-shared card. For example Q-5 is dominated by K-5 or Q-7. In the former case (K-5 over Q-5) only three cards can help Q-5, the other three queens.

That said, the following tables present the probability of every two-card hand being dominated, according to the total number of players.

Probability of Domination — PairsExpand

Cards	2 Players	3 Players	4 Players	5 Players	6 Players	7 Players	8 Players	9 Players	10 Players
2,2	0.0588	0.1142	0.1659	0.2150	0.2609	0.3044	0.3449	0.3835	0.4195
3,3	0.0540	0.1049	0.1532	0.1983	0.2419	0.2826	0.3212	0.3576	0.3922
4,4	0.0489	0.0956	0.1400	0.1820	0.2220	0.2602	0.2966	0.3313	0.3640
5,5	0.0441	0.0862	0.1265	0.1653	0.2021	0.2376	0.2710	0.3031	0.3345
6,6	0.0392	0.0767	0.1133	0.1481	0.1816	0.2136	0.2448	0.2745	0.3036
7,7	0.0344	0.0675	0.0996	0.1306	0.1605	0.1895	0.2177	0.2447	0.2709
8,8	0.0295	0.0581	0.0858	0.1129	0.1391	0.1648	0.1894	0.2138	0.2369
9,9	0.0246	0.0485	0.0720	0.0947	0.1173	0.1391	0.1604	0.1813	0.2017
T,T	0.0196	0.0389	0.0578	0.0765	0.0947	0.1126	0.1300	0.1478	0.1649
J,J	0.0147	0.0293	0.0435	0.0577	0.0719	0.0856	0.0992	0.1132	0.1262
Q,Q	0.0098	0.0195	0.0292	0.0389	0.0483	0.0579	0.0674	0.0766	0.0861
K,K	0.0049	0.0098	0.0147	0.0196	0.0245	0.0294	0.0341	0.0391	0.0439
A,A	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

Probability of Domination — Non-PairsExpand

Cards	2 Players	3 Players	4 Players	5 Players	6 Players	7 Players	8 Players	9 Players	10 Players
3,2	0.2742	0.4785	0.6289	0.7389	0.8187	0.8753	0.9156	0.9438	0.9629
4,2	0.2645	0.4634	0.6124	0.7227	0.8036	0.8626	0.9049	0.9350	0.9562
4,3	0.2496	0.4417	0.5877	0.6986	0.7815	0.8433	0.8888	0.9220	0.9459
5,2	0.2546	0.4487	0.5956	0.7060	0.7881	0.8489	0.8934	0.9255	0.9486
5,3	0.2399	0.4263	0.5701	0.6805	0.7645	0.8279	0.8754	0.9108	0.9367
5,4	0.2253	0.4036	0.5439	0.6539	0.7393	0.8050	0.8556	0.8937	0.9227
6,2	0.2450	0.4338	0.5786	0.6885	0.7718	0.8344	0.8809	0.9152	0.9403
6,3	0.2302	0.4110	0.5525	0.6620	0.7470	0.8118	0.8614	0.8986	0.9266
6,4	0.2154	0.3881	0.5254	0.6344	0.7199	0.7869	0.8394	0.8796	0.9105
6,5	0.2008	0.3647	0.4975	0.6047	0.6911	0.7599	0.8146	0.8581	0.8919
7,2	0.2350	0.4186	0.5611	0.6709	0.7550	0.8191	0.8676	0.9042	0.9311
7,3	0.2204	0.3955	0.5340	0.6430	0.7285	0.7948	0.8461	0.8854	0.9155
7,4	0.2057	0.3724	0.5065	0.6138	0.7000	0.7681	0.8220	0.8642	0.8971
7,5	0.1910	0.3484	0.4776	0.5833	0.6693	0.7388	0.7951	0.8402	0.8761
7,6	0.1763	0.3244	0.4478	0.5510	0.6365	0.7071	0.7651	0.8128	0.8514
8,2	0.2255	0.4034	0.5434	0.6526	0.7375	0.8032	0.8536	0.8923	0.9213
8,3	0.2105	0.3800	0.5157	0.6237	0.7095	0.7771	0.8300	0.8714	0.9034
8,4	0.1959	0.3563	0.4870	0.5932	0.6791	0.7481	0.8037	0.8478	0.8828
8,5	0.1812	0.3323	0.4574	0.5614	0.6467	0.7168	0.7743	0.8208	0.8586
8,6	0.1666	0.3078	0.4272	0.5277	0.6122	0.6829	0.7416	0.7904	0.8311
8,7	0.1518	0.2829	0.3952	0.4922	0.5750	0.6453	0.7056	0.7563	0.7992
9,2	0.2156	0.3878	0.5250	0.6338	0.7194	0.7862	0.8388	0.8793	0.9104
9,3	0.2010	0.3643	0.4968	0.6039	0.6895	0.7583	0.8130	0.8564	0.8904
9,4	0.1862	0.3402	0.4674	0.5720	0.6577	0.7274	0.7843	0.8300	0.8668
9,5	0.1714	0.3157	0.4371	0.5388	0.6234	0.6937	0.7523	0.8003	0.8398
9,6	0.1569	0.2911	0.4061	0.5036	0.5868	0.6573	0.7167	0.7667	0.8088
9,7	0.1419	0.2658	0.3734	0.4669	0.5476	0.6174	0.6776	0.7289	0.7730
9,8	0.1274	0.2403	0.3400	0.4282	0.5061	0.5742	0.6342	0.6867	0.7320
T,2	0.2057	0.3722	0.5066	0.6143	0.7005	0.7688	0.8229	0.8654	0.8987
T,3	0.1910	0.3485	0.4772	0.5831	0.6691	0.7387	0.7950	0.8402	0.8762
T,4	0.1764	0.3240	0.4474	0.5501	0.6352	0.7055	0.7638	0.8111	0.8499
T,5	0.1617	0.2995	0.4163	0.5153	0.5991	0.6696	0.7286	0.7784	0.8196
T,6	0.1470	0.2742	0.3843	0.4790	0.5606	0.6305	0.6904	0.7413	0.7847
T,7	0.1323	0.2487	0.3512	0.4411	0.5196	0.5881	0.6478	0.6996	0.7448
T,8	0.1176	0.2227	0.3169	0.4008	0.4754	0.5418	0.6009	0.6532	0.6993
T,9	0.1030	0.1965	0.2817	0.3586	0.4286	0.4923	0.5492	0.6010	0.6473
J,2	0.1960	0.3566	0.4877	0.5944	0.6808	0.7505	0.8063	0.8508	0.8862
J,3	0.1813	0.3324	0.4578	0.5617	0.6476	0.7180	0.7757	0.8227	0.8610
J,4	0.1665	0.3078	0.4271	0.5275	0.6120	0.6828	0.7419	0.7911	0.8317
J,5	0.1519	0.2827	0.3954	0.4916	0.5741	0.6441	0.7042	0.7549	0.7976
J,6	0.1371	0.2573	0.3621	0.4537	0.5336	0.6026	0.6625	0.7143	0.7590
J,7	0.1223	0.2314	0.3284	0.4142	0.4901	0.5572	0.6164	0.6688	0.7145
J,8	0.1077	0.2050	0.2931	0.3725	0.4442	0.5083	0.5658	0.6174	0.6638
J,9	0.0931	0.1785	0.2571	0.3289	0.3948	0.4553	0.5100	0.5601	0.6061
J,T	0.0783	0.1515	0.2199	0.2837	0.3427	0.3979	0.4493	0.4967	0.5409
Q,2	0.1862	0.3406	0.4685	0.5739	0.6604	0.7312	0.7886	0.8352	0.8727
Q,3	0.1713	0.3161	0.4379	0.5402	0.6255	0.6968	0.7557	0.8044	0.8445
Q,4	0.1568	0.2910	0.4062	0.5045	0.5880	0.6590	0.7189	0.7696	0.8119
Q,5	0.1422	0.2658	0.3736	0.4671	0.5482	0.6180	0.6783	0.7299	0.7744
Q,6	0.1273	0.2400	0.3400	0.4280	0.5055	0.5734	0.6333	0.6857	0.7312
Q,7	0.1126	0.2139	0.3048	0.3868	0.4600	0.5254	0.5835	0.6357	0.6818
Q,8	0.0979	0.1875	0.2691	0.3435	0.4113	0.4730	0.5289	0.5800	0.6257
Q,9	0.0833	0.1606	0.2321	0.2983	0.3600	0.4166	0.4689	0.5173	0.5619
Q,T	0.0687	0.1332	0.1940	0.2516	0.3052	0.3557	0.4032	0.4480	0.4894
Q,J	0.0540	0.1055	0.1547	0.2020	0.2474	0.2902	0.3313	0.3707	0.4082
K,2	0.1763	0.3246	0.4491	0.5532	0.6395	0.7111	0.7702	0.8185	0.8579
K,3	0.1616	0.2998	0.4178	0.5178	0.6027	0.6740	0.7343	0.7848	0.8269
K,4	0.1469	0.2745	0.3851	0.4808	0.5633	0.6343	0.6948	0.7466	0.7908
K,5	0.1322	0.2491	0.3517	0.4422	0.5211	0.5904	0.6509	0.7037	0.7494
K,6	0.1175	0.2230	0.3171	0.4013	0.4763	0.5431	0.6025	0.6550	0.7016
K,7	0.1029	0.1964	0.2814	0.3586	0.4285	0.4918	0.5490	0.6007	0.6473
K,8	0.0881	0.1697	0.2447	0.3139	0.3777	0.4367	0.4905	0.5397	0.5853
K,9	0.0734	0.1423	0.2069	0.2675	0.3238	0.3765	0.4259	0.4720	0.5148
K,T	0.0588	0.1146	0.1678	0.2183	0.2665	0.3120	0.3555	0.3961	0.4350
K,J	0.0441	0.0866	0.1277	0.1671	0.2058	0.2426	0.2780	0.3125	0.3452
K,Q	0.0294	0.0582	0.0865	0.1141	0.1414	0.1679	0.1940	0.2195	0.2444
A,2	0.1665	0.3086	0.4294	0.5316	0.6177	0.6901	0.7505	0.8009	0.8425
A,3	0.1517	0.2835	0.3970	0.4949	0.5791	0.6509	0.7120	0.7641	0.8080
A,4	0.1372	0.2578	0.3636	0.4565	0.5376	0.6082	0.6695	0.7227	0.7684
A,5	0.1224	0.2318	0.3294	0.4164	0.4934	0.5618	0.6223	0.6754	0.7225
A,6	0.1077	0.2054	0.2940	0.3741	0.4462	0.5115	0.5702	0.6228	0.6701
A,7	0.0931	0.1787	0.2575	0.3300	0.3963	0.4572	0.5129	0.5638	0.6101
A,8	0.0783	0.1516	0.2200	0.2837	0.3428	0.3983	0.4498	0.4976	0.5418
A,9	0.0637	0.1241	0.1810	0.2352	0.2866	0.3347	0.3804	0.4237	0.4647
A,T	0.0490	0.0959	0.1411	0.1847	0.2264	0.2664	0.3049	0.3417	0.3770
A,J	0.0343	0.0677	0.1003	0.1320	0.1629	0.1931	0.2223	0.2507	0.2784
A,Q	0.0195	0.0389	0.0582	0.0769	0.0956	0.1140	0.1320	0.1500	0.1676
A,K	0.0049	0.0098	0.0147	0.0195	0.0243	0.0292	0.0340	0.0388	0.0436

Methodology: These tables were created by a random simulation. Each cell in the table above for pairs was based on 7.8 million hands, and 21.7 million for the non-pairs.

2-Player Formula

The probability of domination in a two player game is easy to calculate. For pairs it is 6×(number of higher ranks)/1225. For example, the probability a pair of eights is dominated is 6×6/1225 = 0.0294, because there are six ranks higher than 8 (9,T,J,Q,K,A).

For non-pairs the formula is (6+18×(L-1)+12×H)/1225, where

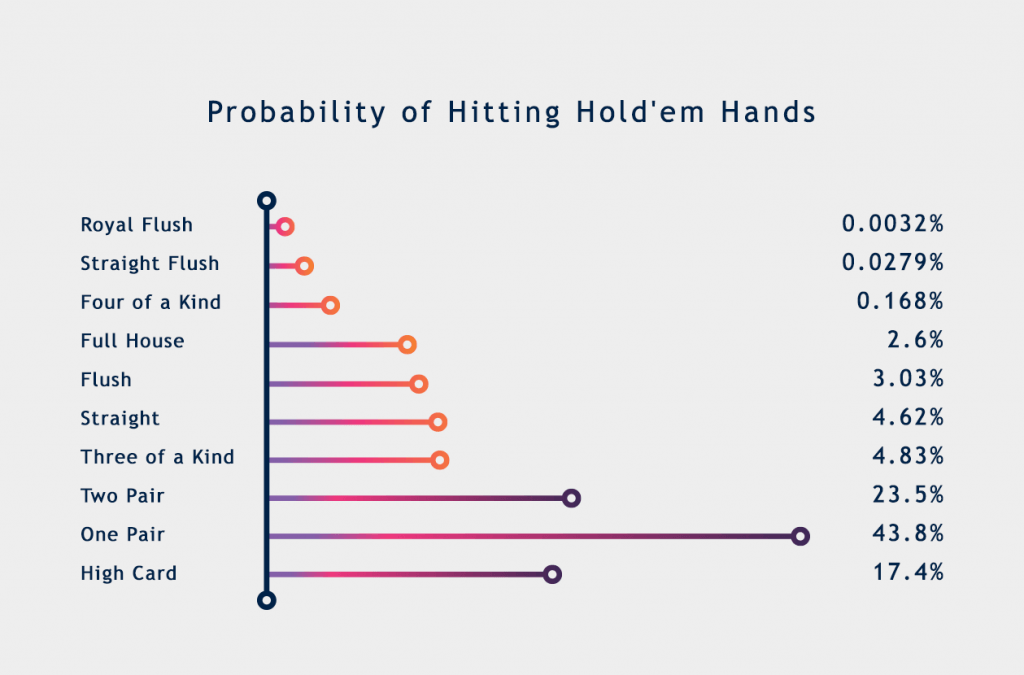
Texas Holdem Hand Odds Probabilities Chart

L=Number of ranks higher than lower card
H=Number of ranks higher than higher card

For example, the probability that J-7 is dominated is (6+18×(7-1)+12×3)/1225 = 150/1225 = 0.1224.

Texas Holdem Hand Odds Probabilities Odds

Written by: Michael Shackleford